While advancements in data science often increase the infamous “skills gap” surrounding the field, Prophet was intentionally designed to lower the cost of entry for “analysts” — who possess an “in-the-loop” understanding of the problems they are trying to solve — via automation of time series forecasting.

Prophet is a procedure for forecasting time series data based on an additive model where non-linear trends are fit with yearly, weekly, and daily seasonality, plus holiday effects. It works best with time series that have strong seasonal effects and several seasons of historical data. Prophet is robust to missing data and shifts in the trend, and typically handles outliers well.
Prophet is open source software released by Facebook’s Core Data Science team. It is available for download on CRAN and PyPI.
The procedure makes use of a decomposable time series model with three main model components: trend, seasonality, and holidays.

y(t) = g(t) + s(t) + h(t) + e(t)
g(t)
- trend models non-periodic changes; linear or logistic
s(t)
- seasonality represents periodic changes; i.e. weekly, monthly, yearly
h(t)
- ties in effects of holidays; on potentially irregular schedules ≥ 1 day(s)
Installation
- pip install pystan
- pip install fbprophet
- conda install -c conda-forge fbprophet
Intro To Facebook Prophet
- Steps
- Initialize Model :: Prophet()
- Set columns as ds,y
- Fit dataset :: Prophet().fit()
- Create Dates To predict :: Prophet().make_future_dataframe(periods=365)
- Predict :: Prophet().predict(future_dates)
- Plot :: Prophet().plot(predictions)
In [ ]:
# Load EDA Pkgs import pandas as pd import matplotlib.pyplot as plt %matplotlib inline
In [ ]:
# Load FB Prophet import fbprophet
In [ ]:
dir(fbprophet)
Out[ ]:
['Prophet', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', '__version__', 'diagnostics', 'forecaster', 'hdays', 'make_holidays', 'models', 'plot']
In [ ]:
# Load our Dataset
df = pd.read_csv("flights_data.csv")
In [ ]:
df.head()
Out[ ]:
| Dates | no_of_flights | |
|---|---|---|
| 0 | 2005-01-01 | 594924 |
| 1 | 2005-02-01 | 545332 |
| 2 | 2005-03-01 | 617540 |
| 3 | 2005-04-01 | 594492 |
| 4 | 2005-05-01 | 614802 |
In [ ]:
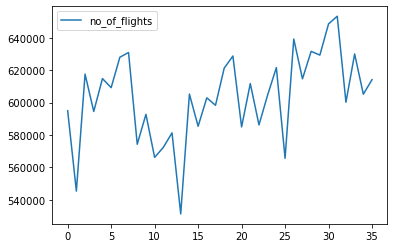
df.plot()
Out[ ]:
<matplotlib.axes._subplots.AxesSubplot at 0x21ac5193988>
In [ ]:
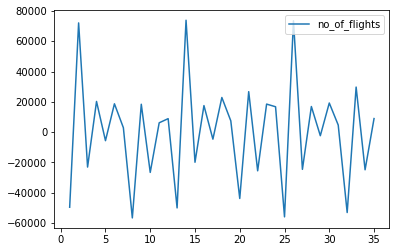
#yt = yt -y(t-1) df['no_of_flights'] = df['no_of_flights'] - df['no_of_flights'].shift(1)
In [ ]:
df.plot()
Out[ ]:
<matplotlib.axes._subplots.AxesSubplot at 0x21ac5300188>
In [ ]:
from fbprophet import Prophet
In [ ]:
# Features of Prophet dir(Prophet)
Out [ ]:
['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', '_load_stan_backend', 'add_country_holidays', 'add_group_component', 'add_regressor', 'add_seasonality', 'construct_holiday_dataframe', 'fit', 'fourier_series', 'initialize_scales', 'linear_growth_init', 'logistic_growth_init', 'make_all_seasonality_features', 'make_future_dataframe', 'make_holiday_features', 'make_seasonality_features', 'parse_seasonality_args', 'percentile', 'piecewise_linear', 'piecewise_logistic', 'plot', 'plot_components', 'predict', 'predict_seasonal_components', 'predict_trend', 'predict_uncertainty', 'predictive_samples', 'regressor_column_matrix', 'sample_model', 'sample_posterior_predictive', 'sample_predictive_trend', 'set_auto_seasonalities', 'set_changepoints', 'setup_dataframe', 'validate_column_name', 'validate_inputs']
In [ ]:
# Initialize the Model model = Prophet()
Parameters
- growth: linear/logistic
- seasonality:additive/multiplicative
- holidays:
- changepoint:
df.columns
Out[ ]:
Index(['Dates', 'no_of_flights'], dtype='object')
In [ ]:
# Works with a ds and y column names
df.rename(columns={'Dates':'ds','no_of_flights':'y'},inplace=True)
In [ ]:
df.head()
Out[ ]:
| ds | y | |
|---|---|---|
| 0 | 2005-01-01 | NaN |
| 1 | 2005-02-01 | -49592.0 |
| 2 | 2005-03-01 | 72208.0 |
| 3 | 2005-04-01 | -23048.0 |
| 4 | 2005-05-01 | 20310.0 |
In [ ]:
df = df[1:]
In [ ]:
df.head()
Out[ ]:
| ds | y | |
|---|---|---|
| 1 | 2005-02-01 | -49592.0 |
| 2 | 2005-03-01 | 72208.0 |
| 3 | 2005-04-01 | -23048.0 |
| 4 | 2005-05-01 | 20310.0 |
| 5 | 2005-06-01 | -5607.0 |
In [ ]:
# Fit our Model to our Data model.fit(df)
Out[ ]:
<fbprophet.forecaster.Prophet at 0x21ac544de08>
In [ ]:
# Shape of Dataset df.shape
Out[ ]:
(35, 2)
In [ ]:
# Create Future Dates of 365 days future_dates = model.make_future_dataframe(periods=365)
In [ ]:
# Shape after adding 365 days future_dates.shape
Out[ ]:
(400, 1)
In [ ]:
future_dates.head()
Out[56]:
| ds | |
|---|---|
| 0 | 2005-02-01 |
| 1 | 2005-03-01 |
| 2 | 2005-04-01 |
| 3 | 2005-05-01 |
| 4 | 2005-06-01 |
In [ ]:
# Make Prediction with our Model prediction = model.predict(future_dates)
In [ ]:
prediction.head()
Out[ ]:
| ds | trend | yhat_lower | yhat_upper | trend_lower | trend_upper | additive_terms | additive_terms_lower | additive_terms_upper | yearly | yearly_lower | yearly_upper | multiplicative_terms | multiplicative_terms_lower | multiplicative_terms_upper | yhat | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2005-02-01 | -2571.714150 | -52813.083521 | -46164.594330 | -2571.714150 | -2571.714150 | -46882.135892 | -46882.135892 | -46882.135892 | -46882.135892 | -46882.135892 | -46882.135892 | 0.0 | 0.0 | 0.0 | -49453.850042 |
| 1 | 2005-03-01 | -2445.189985 | 67319.743206 | 74045.134070 | -2445.189985 | -2445.189985 | 73145.012894 | 73145.012894 | 73145.012894 | 73145.012894 | 73145.012894 | 73145.012894 | 0.0 | 0.0 | 0.0 | 70699.822909 |
| 2 | 2005-04-01 | -2305.109659 | -27300.668683 | -20707.417240 | -2305.109659 | -2305.109659 | -21686.914066 | -21686.914066 | -21686.914066 | -21686.914066 | -21686.914066 | -21686.914066 | 0.0 | 0.0 | 0.0 | -23992.023726 |
| 3 | 2005-05-01 | -2169.548054 | 14332.149718 | 21283.340405 | -2169.548054 | -2169.548054 | 19993.464271 | 19993.464271 | 19993.464271 | 19993.464271 | 19993.464271 | 19993.464271 | 0.0 | 0.0 | 0.0 | 17823.916217 |
| 4 | 2005-06-01 | -2029.467726 | -10647.000844 | -3755.469838 | -2029.467726 | -2029.467726 | -5302.735919 | -5302.735919 | -5302.735919 | -5302.735919 | -5302.735919 | -5302.735919 | 0.0 | 0.0 | 0.0 | -7332.203646 |
Narrative
- yhat : the predicted forecast
- yhat_lower : the lower border of the prediction
- yhat_upper: the upper border of the prediction
In [ ]:
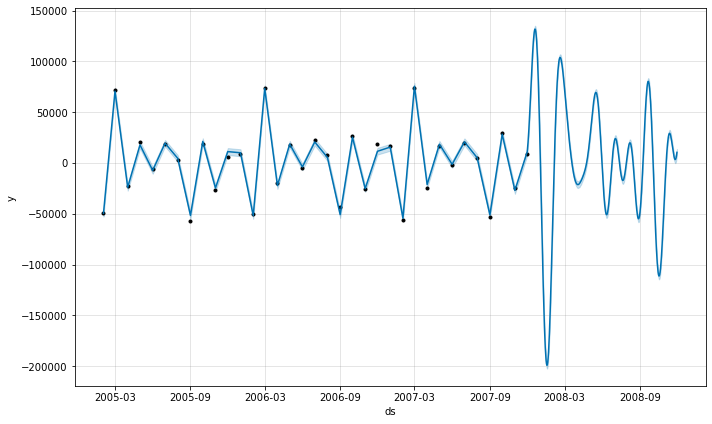
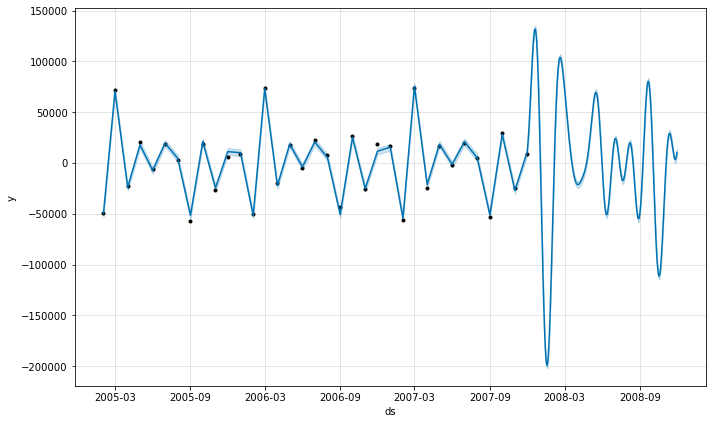
# Plot Our Predictions model.plot(prediction)
Out[ ]:
Narrative
- A Trending data
- Black dots : the actual data points in our dataset.
- Deep blue line : the predicted forecast/the predicted values
- Light blue line : the boundaries
In [ ]:
# Visualize Each Component [Trends,Weekly] model.plot_components(prediction)
Out[ ]:
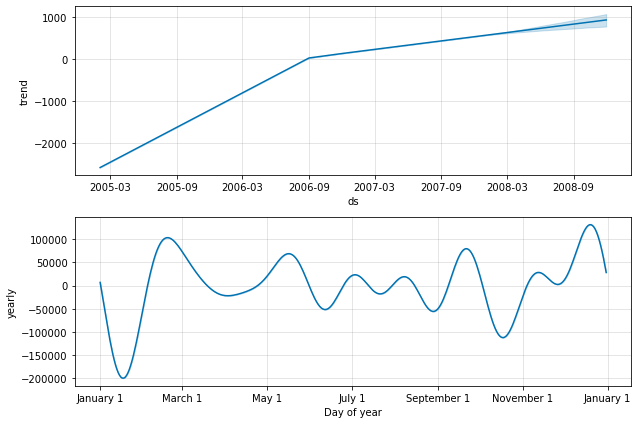
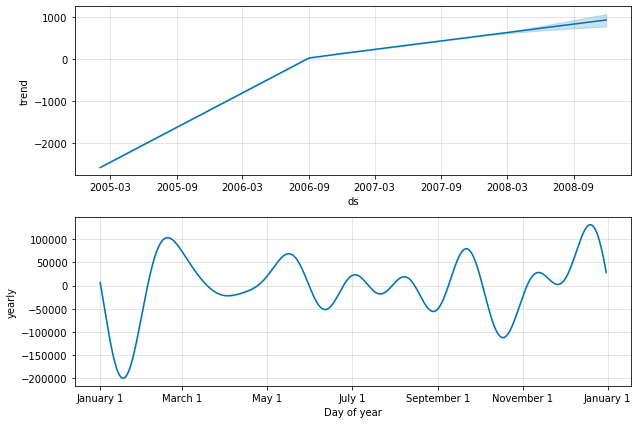
Cross Validation
- For measuring forecast error by comparing the predicted values with the actual values
- initial:the size of the initial training period
- period : the spacing between cutoff dates
- horizon : the forecast horizon((ds minus cutoff)
- By default, the initial training period is set to three times the horizon, and cutoffs are made every half a horizon
In [ ]:
# Load Pkgs from fbprophet.diagnostics import cross_validation
In [ ]:
df.shape
Out[ ]:
(35, 2)
In [ ]:
cv = cross_validation(model,initial='35 days', period='180 days', horizon = '365 days')
In [ ]:
cv.head()
Out[ ]:
| ds | yhat | yhat_lower | yhat_upper | y | cutoff | |
|---|---|---|---|---|---|---|
| 0 | 2005-07-01 | -2.998956e+05 | -2.998956e+05 | -2.998956e+05 | 18766.0 | 2005-06-09 |
| 1 | 2005-08-01 | -1.506471e+06 | -1.506471e+06 | -1.506471e+06 | 2943.0 | 2005-06-09 |
| 2 | 2005-09-01 | 4.293684e+03 | 4.293683e+03 | 4.293685e+03 | -56651.0 | 2005-06-09 |
| 3 | 2005-10-01 | 1.213440e+06 | 1.213440e+06 | 1.213440e+06 | 18459.0 | 2005-06-09 |
| 4 | 2005-11-01 | -2.180407e+05 | -2.180407e+05 | -2.180407e+05 | -26574.0 | 2005-06-09 |
Performance Metrics
In [ ]:
from fbprophet.diagnostics import performance_metrics
In [ ]:
df_pm = performance_metrics(cv)
In [ ]:
df_pm
Out[ ]:
| horizon | mse | rmse | mae | mape | mdape | coverage | |
|---|---|---|---|---|---|---|---|
| 0 | 31 days | 2.692910e+10 | 164100.895645 | 102813.813574 | 6.589854 | 4.597027 | 0.00 |
| 1 | 53 days | 5.711252e+11 | 755728.239683 | 400501.823432 | 130.565316 | 4.597027 | 0.00 |
| 2 | 57 days | 5.827072e+11 | 763352.591903 | 438304.026472 | 129.539674 | 2.545742 | 0.00 |
| 3 | 58 days | 5.826882e+11 | 763340.159421 | 437355.801093 | 129.680706 | 2.827806 | 0.00 |
| 4 | 62 days | 5.827802e+11 | 763400.445519 | 441439.714453 | 129.721404 | 2.827806 | 0.00 |
| 5 | 84 days | 1.412643e+10 | 118854.679447 | 79322.480541 | 1.769691 | 1.079564 | 0.00 |
| 6 | 85 days | 1.410763e+10 | 118775.525681 | 79281.360860 | 1.399342 | 1.079564 | 0.00 |
| 7 | 89 days | 1.409591e+10 | 118726.194857 | 78341.366537 | 1.153351 | 0.711576 | 0.25 |
| 8 | 90 days | 1.406118e+10 | 118579.838784 | 77345.962716 | 1.119003 | 0.642882 | 0.25 |
| 9 | 114 days | 3.701274e+11 | 608380.996828 | 360855.010334 | 17.034313 | 1.650424 | 0.25 |
| 10 | 116 days | 3.671415e+11 | 605922.017604 | 353902.099998 | 18.788783 | 5.159363 | 0.25 |
| 11 | 119 days | 3.671453e+11 | 605925.155903 | 354275.099608 | 18.818494 | 5.163485 | 0.25 |
| 12 | 121 days | 3.671874e+11 | 605959.904282 | 355456.777691 | 18.971425 | 5.465225 | 0.25 |
| 13 | 145 days | 1.935746e+10 | 139131.074345 | 104578.230658 | 4.588426 | 4.013367 | 0.25 |
| 14 | 146 days | 2.208847e+10 | 148621.914355 | 110970.887685 | 5.282878 | 4.013367 | 0.25 |
| 15 | 150 days | 2.220278e+10 | 149005.973914 | 115051.650741 | 5.445470 | 4.036810 | 0.00 |
| 16 | 151 days | 2.211875e+10 | 148723.733688 | 112115.362158 | 5.364398 | 4.036810 | 0.00 |
| 17 | 175 days | 6.795244e+10 | 260676.880961 | 181507.549788 | 22.460618 | 6.877573 | 0.00 |
| 18 | 177 days | 6.598742e+10 | 256880.170222 | 176987.165501 | 30.550315 | 23.056968 | 0.00 |
| 19 | 180 days | 6.586463e+10 | 256641.044587 | 171556.031290 | 30.339130 | 22.871380 | 0.25 |
| 20 | 182 days | 6.586411e+10 | 256640.037341 | 171525.164837 | 31.107120 | 24.407360 | 0.25 |
| 21 | 206 days | 8.747295e+10 | 295758.254878 | 192656.511929 | 27.682607 | 24.407360 | 0.25 |
| 22 | 207 days | 9.046698e+10 | 300777.288635 | 199405.667040 | 18.936865 | 6.915876 | 0.25 |
| 23 | 211 days | 9.049226e+10 | 300819.307680 | 201811.347581 | 19.080676 | 6.915876 | 0.25 |
| 24 | 212 days | 9.054020e+10 | 300898.979715 | 203770.930708 | 18.397766 | 5.550056 | 0.25 |
| 25 | 237 days | 3.058308e+10 | 174880.177196 | 129898.701032 | 4.214128 | 2.997520 | 0.25 |
| 26 | 238 days | 2.773357e+10 | 166533.989174 | 123495.298167 | 8.649487 | 2.997520 | 0.25 |
| 27 | 242 days | 2.772052e+10 | 166494.800664 | 122730.874808 | 8.531024 | 2.997520 | 0.25 |
| 28 | 243 days | 2.770857e+10 | 166458.918733 | 122342.336413 | 9.094915 | 4.125301 | 0.25 |
| 29 | 265 days | 2.421694e+10 | 155617.925574 | 115179.927020 | 8.580976 | 3.097424 | 0.25 |
| 30 | 269 days | 2.778923e+10 | 166701.023204 | 123099.628298 | 2.957869 | 3.097424 | 0.25 |
| 31 | 270 days | 2.777735e+10 | 166665.386503 | 121662.571302 | 2.930838 | 3.097424 | 0.25 |
| 32 | 274 days | 2.792908e+10 | 167119.947533 | 125172.096410 | 2.292353 | 1.820456 | 0.25 |
| 33 | 296 days | 3.008901e+10 | 173461.837321 | 129700.647719 | 4.632041 | 3.025373 | 0.25 |
| 34 | 299 days | 2.284019e+10 | 151129.725412 | 112125.261120 | 4.851126 | 3.463543 | 0.25 |
| 35 | 301 days | 2.284588e+10 | 151148.551953 | 113044.048809 | 4.897076 | 3.463543 | 0.25 |
| 36 | 304 days | 2.266595e+10 | 150552.134430 | 108388.015932 | 4.846210 | 3.361811 | 0.25 |
| 37 | 326 days | 2.142954e+10 | 146388.325580 | 105838.063764 | 5.108533 | 3.361811 | 0.25 |
| 38 | 330 days | 3.116496e+10 | 176536.007400 | 128361.570161 | 6.069923 | 5.284592 | 0.25 |
| 39 | 331 days | 3.116747e+10 | 176543.098562 | 128593.470506 | 6.106102 | 5.289459 | 0.25 |
| 40 | 335 days | 3.114527e+10 | 176480.218194 | 126935.924115 | 6.056153 | 5.289459 | 0.50 |
| 41 | 357 days | 3.485784e+10 | 186702.551971 | 134300.237280 | 17.165825 | 5.289459 | 0.50 |
| 42 | 360 days | 2.386630e+10 | 154487.217191 | 107932.593538 | 16.704551 | 4.366910 | 0.50 |
| 43 | 362 days | 2.386316e+10 | 154477.050064 | 107634.307044 | 17.119322 | 5.196453 | 0.50 |
| 44 | 365 days | 2.400036e+10 | 154920.493560 | 112706.360327 | 17.743509 | 5.510519 | 0.25 |
Visualizing Performance Metrics
- cutoff: how far into the future the prediction was
In [ ]:
from fbprophet.plot import plot_cross_validation_metric
In [ ]:
plot_cross_validation_metric(cv,metric='rmse')
Out[ ]:
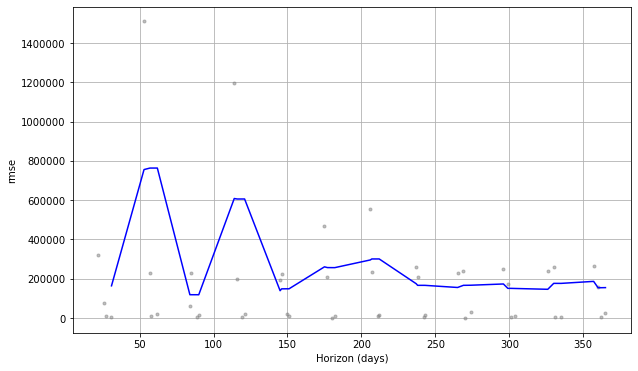
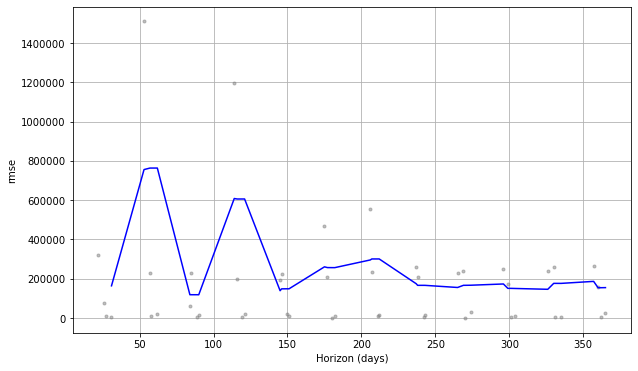
Leave a Reply